Skip to main content

Mock 002

Bishal's Maths Tuition (+91-8910047668)

MATHEMATICS​

CLASS X CBSE Board​

Time allowed : 2.5 hours​
Maximum Marks : 80 ​

General Instructions : Read the following instructions very carefully and strictly follow them :
(i) This question paper comprises four sections - A, B, C and D. This question paper carries 40 questions. All questions are compulsory.
(ii) Section A : Question Numbers 1 to 20 comprises of 20 questions of one mark each.
(iii) Section B : Question Numbers 21 to 26 comprises of 6 questions of two marks each.
(iv) Section C : Question Numbers 27 to 34 comprises of 8 questions of three marks each.
(v) Section D : Question Numbers 35 to 40 comprises of 6 questions of four marks each.
(vi) There is no overall choice in the question paper. However, an internal choice has been provided in 2 questions of one mark, 2 questions of two marks, questions of three marks and 2 questions of four marks. You have to attempt only one of the choices in such questions.
(vii) In addition to this, separate instructions are given with each section and question, wherever necessary.
(viii) Use of calculators is not permitted.

SECTION – A​

marks

Question numbers 1 to 20 carry 1 mark each.

  1. Find the value(s) of kk for which the quadratic equation 2x2+kx+2=02x^2 + kx + 2 = 0 has equal roots.

  2. Which of the following is not an A.P. ?

    1. −1⋅2,0⋅8,2⋅8,...- 1·2, 0·8, 2·8, ...
    2. 3,3+2,3+22,3+32,...3,3+\sqrt 2,3+2\sqrt 2,3+3\sqrt 2,...
    3. 47,73,93,123,...\dfrac{4}{7}, \dfrac{7}{3}, \dfrac{9}{3}, \dfrac{12}{3},...
    4. −15,−25,−35,...\dfrac{-1}{5}, \dfrac{-2}{5}, \dfrac{-3}{5},...

  3. Find the radius of a sphere (in cm) whose volume is 12πcm312\pi cm^3.

  4. Find the distance between the points (m,−n)(m, - n) and (−m,n)(- m, n).

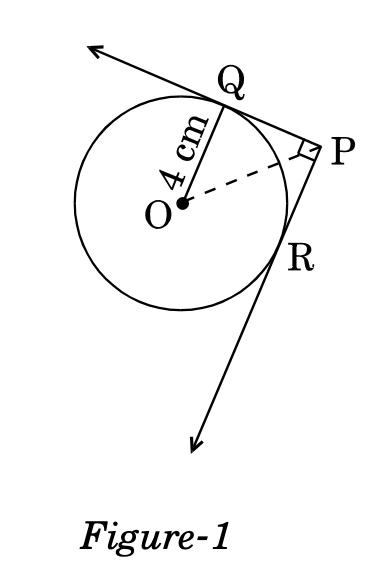
  5. In Figure-1, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. If ∠QPR=90°\angle QPR = 90\degree, then find the length of PQ

  6. On dividing a polynomial p(x)p(x) by x2−4x^2 - 4, quotient and remainder are found to be xx and 33 respectively. Find the polynomial p(x)p(x)

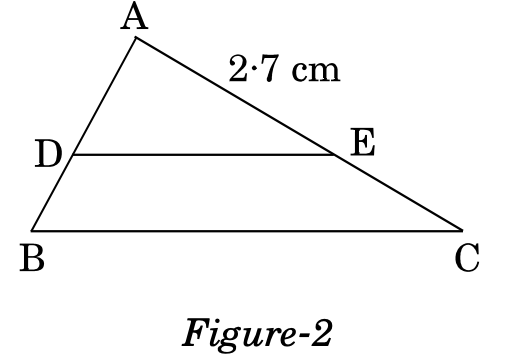
  7. In Figure-2, DE∥BCDE \parallel BC. If ADDB=32\dfrac{AD}{DB} =\dfrac{3}{2} and AE=2⋅7cmAE = 2·7 cm, then find ECEC

  8. Find the point on the x-axis which is equidistant from (−4,0)(- 4, 0) and (10,0)(10, 0).
    OR
    Find the centre of a circle whose end points of a diameter are (−6,3)(- 6, 3) and (6,4)(6, 4)

  9. The pair of linear equations 3x2+5y3=7\dfrac{3x}{2} + \dfrac{5y}{3} = 7 and 9x+10y=149x + 10y = 14 is

    1. consistent
    2. inconsistent
    3. consistent with one solution
    4. consistent with many solutions

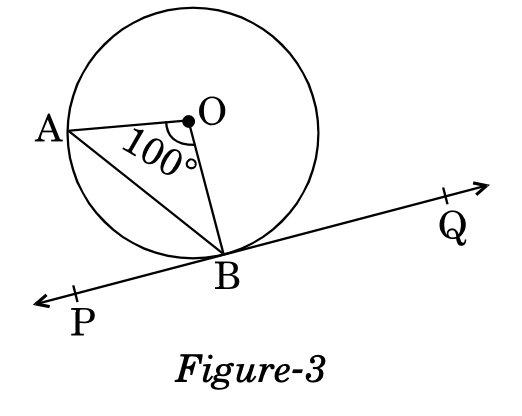
  10. In Figure-3, PQPQ is tangent to the circle with centre at OO, at the point BB. If ∠AOB=100°\angle AOB = 100\degree, then find ∠ABP\angle ABP.

  11. Find simplest form of 1+tan⁡2A1+cot⁡2A\dfrac{1 + \tan^2 A}{1 + \cot^2 A}

  12. Find P(E‾)P(\overline{E}), If the probability of an event EE happening is 0⋅0230·023

  13. All concentric circles are ------------- to each other.

  14. The probability of an event that is sure to happen, is --------------- .

  15. AOBCAOBC is a rectangle whose three vertices are A(0,−3)A(0, -3), O(0,0)O(0, 0) and B(4,0)B(4, 0). Find the length of its diagonal.

  16. Write the value of sin230°+cos260°sin^2 30\degree + cos^2 60\degree.

  17. Form a quadratic polynomial, the sum and product of whose zeroes are (−3)(- 3) and 22 respectively.
    OR
    Can (x2−1)(x^2 - 1) be a remainder while dividing x4−3x2+5x−9x^4 - 3x^2 + 5x - 9 by (x2+3)(x^2 + 3) ? Justify your answer with reasons.

  18. Find the sum of the first 100 natural numbers.

  19. The LCM of two numbers is 182 and their HCF is 13. If one of the numbers is 26, find the other.

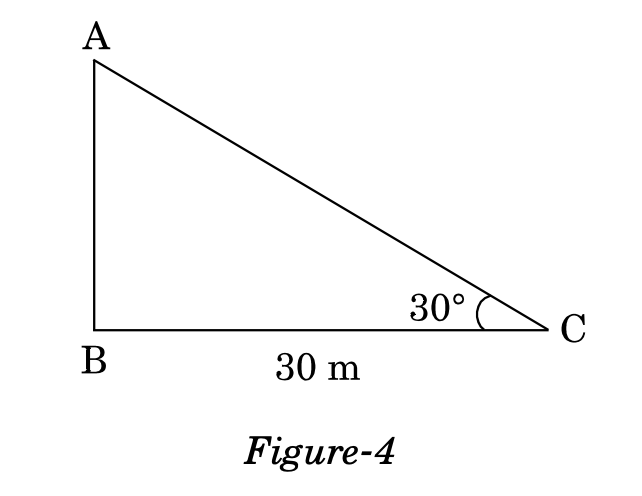
  20. In Figure-4, the angle of elevation of the top of a tower from a point C on the ground, which is 30 m away from the foot of the tower, is 30°30\degree. Find the height of the tower.

SECTION – B​

marks

Question numbers 21 to 26 carry 2 marks each.

  1. A cone and a cylinder have the same radii but the height of the cone is 3 times that of the cylinder. Find the ratio of their volumes.

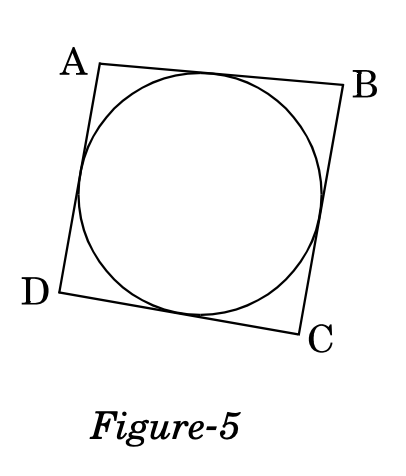
  2. In Figure-5, a quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=BC+ADAB + CD = BC + AD.

    OR
    In Figure-6, find the perimeter of 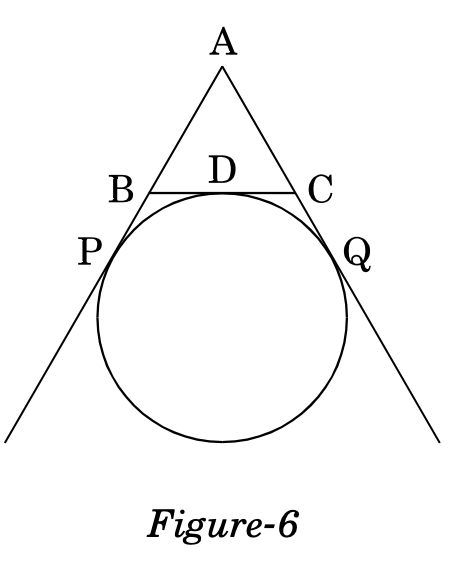ΔABC\Delta ABC, if AP=12cmAP = 12 cm.

  3. Find the mode of the following distribution :

Marks :0 – 1010 – 2020 – 3030 – 4040 – 5050 – 60
Number of Students :4671256
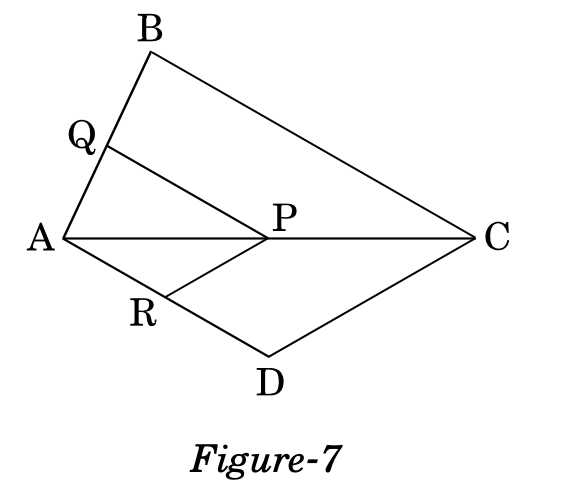
  1. In Figure-7, if PQ∥BCPQ \parallel BC and PR∥CDPR \parallel CD, prove that QBAQ=DRAR\dfrac{QB}{AQ} = \dfrac{DR}{AR}.
  2. Show that 5+275 + 2\sqrt 7 is an irrational number, where 7\sqrt 7 is given to be an irrational number.
    OR
    Check whether 12n12^n can end with the digit 0 for any natural number nn.
  3. If A,BA, B and CC are interior angles of a ΔABC\Delta ABC, then show that
    cos⁡(B+C2)=sin⁡(A2)\cos \left( \dfrac{B+C}{2} \right) = \sin \left( \dfrac{A}{2} \right)

SECTION – C​

marks

Question numbers 27 to 34 carry 3 marks each.

  1. Prove that : (sin⁡4θ−cos⁡4θ+1)cosec⁡2θ=2(\sin^4 \theta - \cos^4 \theta + 1) \cosec^2 \theta = 2

  2. Find the sum : (−5)+(−8)+(−11)+...+(−230)(- 5) + (- 8) + (- 11) + ... + (- 230)

  3. Construct a ΔABC\Delta ABC with sides BC=6cmBC=6cm, AB=5cmAB=5cm and ∠ABC=60°\angle ABC=60\degree. Then construct a triangle whose sides are 34\dfrac{3}{4} of the corresponding sides of ΔABC\Delta ABC
    OR
    Draw a circle of radius 3·5 cm. Take a point P outside the circle at a distance of 7 cm from the centre of the circle and construct a pair of tangents to the circle from that point.

  4. In Figure-8, ABCD is a parallelogram. A semicircle with centre O and the diameter AB has been drawn and it passes through D. If AB = 12 cm and OD ⊥\bot AB, then find the area of the shaded region. (Use π\pi = 3·14)

  5. Read the following passage and answer the questions given at the end :
    Diwali Fair
    A game in a booth at a Diwali Fair involves using a spinner first. Then, if the spinner stops on an even number, the player is allowed to pick a marble from a bag. The spinner and the marbles in the bag are represented in Figure-9.
    Prizes are given, when a black marble is picked. Shweta plays the game once.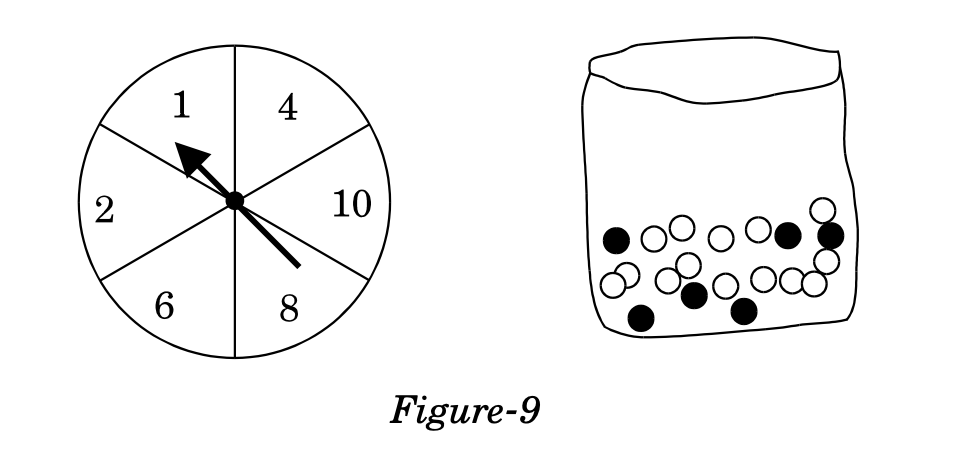

  • What is the probability that she will be allowed to pick a marble from the bag ?
  • Suppose she is allowed to pick a marble from the bag, what is the probability of getting a prize, when it is given that the bag contains 20 balls out of which 6 are black ?
  1. A fraction becomes 13\dfrac{1}{3} when 1 is subtracted from the numerator and it becomes 14\dfrac{1}{4} when 8 is added to its denominator. Find the fraction.
    OR
    The present age of a father is three years more than three times the age of his son. Three years hence the father’s age will be 10 years more than twice the age of the son. Determine their present ages.
  2. Find the ratio in which the y-axis divides the line segment joining the points (6,−4)(6, - 4) and (−2,−7)(- 2, - 7). Also find the point of intersection.
    OR
    Show that the points (7,10)(7, 10), (−2,5)(- 2, 5) and (3,−4)(3, - 4) are vertices of an isosceles right triangle.
  3. Use Euclid Division Lemma to show that the square of any positive integer is either of the form 3q3q or 3q+13q + 1 for some integer qq.

SECTION – D​

marks

Question numbers 35 to 40 carry 4 marks each.

  1. Sum of the areas of two squares is 544m2544 m^2. If the difference of their perimeters is 32m32 m, find the sides of the two squares.
    OR
    A motorboat whose speed is 18km/h18 km/h in still water takes 1 hour more to go 24km24 km upstream than to return downstream to the same spot. Find the speed of the stream.
  2. For the following data, draw a ‘less than’ ogive and hence find the median of the distribution.
Age(in years) :0 – 1010 – 2020 – 3030 – 4040 – 5050 – 6060 – 70
Number of persons :515202515119
  1. A statue 1·6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60°60\degree and from the same point the angle of elevation of the top of the pedestal is 45°45 \degree. Find the height of the pedestal. (Use 3=1⋅73\sqrt 3 = 1·73)
  2. Obtain other zeroes of the polynomial p(x)=2x4−x3−11x2+5x+5p(x) = 2x^4 - x^3 - 11x^2 + 5x + 5 if two of its zeroes are 55 and −5- 5.
    OR
    What minimum must be added to 2x3−3x2+6x+72x^3 - 3x^2 + 6x + 7 so that the resulting polynomial will be divisible by x2−4x+8x^2 - 4x + 8 ?
  3. In a cylindrical vessel of radius 10 cm, containing some water, 9000 small spherical balls are dropped which are completely immersed in water which raises the water level. If each spherical ball is of radius 0·5 cm, then find the rise in the level of water in the vessel.
  4. If a line is drawn parallel to one side of a triangle to intersect the other two sides at distinct points, prove that the other two sides are divided in the same ratio.